Aprenda distinguir rapidamente os sinais de maior que e menor que e tire de suas dúvidas.
Quando se estuda língua portuguesa aprende-se diversos sinais como letras, acentos e pontuação que, ao serem usados dentro das regras pré-estabelecidas, constroem palavras e frases. Na matemática isso não é diferente.
Juntamente com os números, os símbolos matemáticos possuem suas funções distintas dentro das operações, e ao serem compreendidos, facilitam o entendimento de quem busca aprender cálculo.
Alguns são mais simples, e comumente utilizados, como o sinal de mais (+), por exemplo. Ele tem o poder de somar duas ou mais numerações gerando um resultado. Enquanto o sinal de menos (-) tem a função de subtrair, retirar, um valor de outro. Mas, dependendo da equação, ele pode aparecer apenas para simbolizar que o valor de um determinado número é negativo.
Já os símbolos de maior que (>) e menor que (<), assim como o sinal de igual a (=), chamados de sinais de relação, tem função mais específica, embora sejam igualmente simples. O primeiro a surgir foi o símbolo de igualmente, utilizado pela primeira vez pelo matemático inglês Robert Recorde. Já os sinais de grandezas distintas surgiram a partir das pesquisas de análise algébrica de Thomaz Harriot.
Sinal de maior que e menor que
O significam os símbolos maior que e menor que?
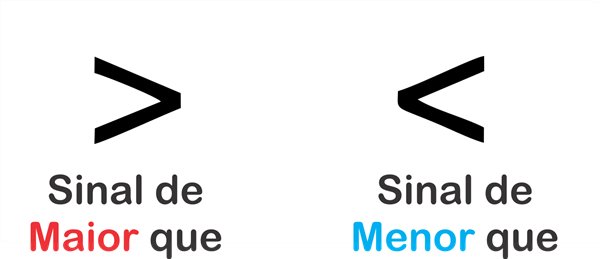
Como foi dito anteriormente, os símbolos de maior que (>) e menor que (<) são conhecidos como sinais de relação matemáticos. Ou seja, servem para comparar os valores, indicando a grandeza entre eles.
O sinal de maior que (>) sempre será utilizado para demonstrar que o número posicionado à esquerda da sentença tem valor numérico maior que o número à direita. O mesmo vale para o menor que (<), que indica que o número posicionado à esquerda tem valor numérico menor que o número à direita.
Quando os sinais maior que e menor que devem ser utilizados?
A utilização dos símbolos maior que (>) e menor que (<) caracteriza a sentença como uma inequação, ou seja, uma relação entre duas representações algébricas mediante uma desigualdade. Para facilitar o entendimento, enquanto uma equação tem resultados exatos iguais a, uma inequação traz resultados desiguais de valores maiores que ou menores que.
As inequações são comumente encontradas em exercícios de função.
Sinais de menor que e maior que com traço
Em algumas inequações, os sinais de maior que (>) e menor que (<) surgem com um pequeno traço embaixo. Este traço em questão significa que o resultado poder maior ou igual (≥) ao valor resultante, ou menor ou igual (≤), dependendo do símbolo que acompanha a sentença.
Logo o resultado permanece sendo um valor desigual, porém possui a possibilidade de ser também uma igualdade. Por exemplo, se x for maior ou igual a 8, significa que x pode ser substituído por qualquer número maior que 8, ou por ele próprio, sem causar alteração no resultado da sentença.
Dica para decorar
Embora o conceito desses símbolos seja simples, muitas pessoas acabam confundindo a utilização dos sinais, podendo alterar completamente o resultado final. E para que isso não aconteça mais, existem duas formas fáceis de lembrar qual sinal usar.
A primeira resume-se em lembrar que a parte aberta do sinal sempre ficará de frente para o número de maior valor. Nas escolas esse método é ensinado como a boca de um jacaré, pois o animal sempre irá querer comer a maior porção de carne, logo virará sua boca aberta para ela. Por exemplo: 3 < 7 (três é menor que sete) e 7 > 3 (sete é maior que três).
A segunda, e ainda mais simples, consiste em fazer um traço na vertical na linha inferior dos símbolos para que eles lembrem os números 7 e 4. Ou seja, o maior que (>) ao ser traçado fica parecendo com um 7 disforme, enquanto o menor que (<) fica parecido com um 4. Sete é maior do que quatro, logo > representa maior e < representa menor. Assim, sempre que houver uma dúvida basta usar esse método para ter certeza de qual sinal utilizar.

Atividades matemáticas com o uso de maior que é menor que
Função de 1° grau
Dada a função f(x) = 2x – 1, se f(x) > 3, pode-se dizer então:
2x – 1 > 3 sendo está uma inequação de 1° grau
2x > 3 + 1
2x > 4
x > 4 : 2
x > 2 o que significa que para essa função ser verdadeira o valor de x pode ser qualquer número de valor maior que 2.
Ou
Dada a função f(x) = 2(x – 2), sendo que f(x) ≥ 4x -2.
Logo
2(x -2) ≥ 4x -2
2x -4 ≥ 4x – 2 Aqui os termos semelhantes são unidos
2x – 4x ≥ -2 + 4
-2x ≥ 2 Toda a inequação é multiplica por -1 para obter a inversão dos sinais, isso inclui o sinal de maior ou igual
2x ≤ -2
x ≤ -1 Assim x pode assumir qualquer valor que seja menor ou igual a -1.
Inequação de 1° grau
Dada a inequação 2x + 8 < 0, pode-se dizer então:
2x < -8
x < -8 : 2
x < -4 logo essa inequação será verdadeira sempre que x for substituído por qualquer número menor que -4.
Ou
Dada a inequação 2x/3 + 6 ≥ x/5 + 9 pode-se dizer então:
2x/3 – x/5 + 6 ≥ x/5 – x/5 + 9
10x – 3x/15 + 6 ≥ 9
7x/15 + 6 ≥ 9
7x/15 + 6 – 6 ≥ 9 – 6
7x/15 ≥ 3 Nesse ponto multiplica-se pela fração inversa
(15/7) x 7x/15 ≥ 3 x (15/7) Ao simplificar as frações chega-se ao resultado
x ≥ 45/7
Quer aprender um pouco mais sobre matemática? Veja uma dica para aprender a formar algarismos romanos de 1 a 5000 rapidamente.